Solvers for ordinary differential equations (ODEs) belong to the best-studied algorithms of numerical mathematics. An ODE is an implicit statement about the relationship of a curve $x:\mathbb{R}_{\geq 0}\to\mathbb{R}^N$ to its derivative, in the form $x'(t) = f(x(t),t)$, where $x'$ is the derivative of curve, and $f$ is some function. To identify a unique solution of a particular ODE, it is typically also necessary to provide additional statements about the curve, such as its initial value $x(t_0)=x_0$. An ODE solver is a mathematical rule that maps function and initial value, $(f,x_0)$ to an estimate $x(t)$ for the solution curve. Good solvers have certain analytical guarantees about this estimate, such as the fact that its deviation from the true solution is of a high polynomial order in the step size used by the algorithms to discretize the ODE.
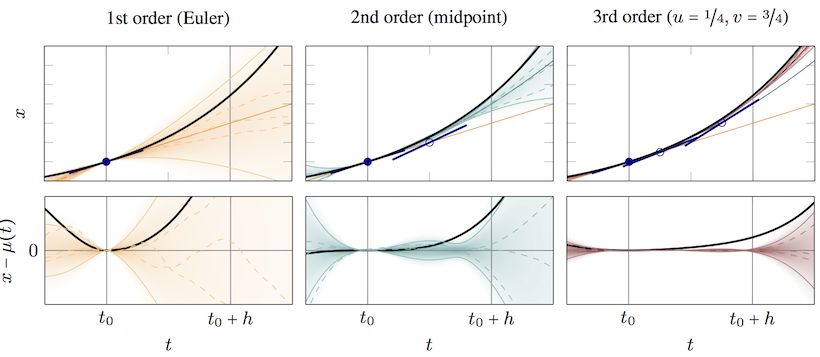
One of the main theoretical contributions of the group is the development of probabilistic versions of these solvers. In several works, we established a class of solvers for initial value problems that generalize classic solvers by taking as inputs Gaussian distributions $\mathcal{N}(x(t_0);x_0,\Psi)$, $\mathcal{GP}(f;\hat{f},\Sigma)$ over the initial value and vector field, and return a Gaussian process posterior $\mathcal{GP}(x;m,k)$ over the solution. We were able to show that these methods
- have the same (linear) computational computational complexity in solver's step-size $h$ as classic methods [ ] (they are Bayesian filters)
- can inherit the famous local and global polynomial convergence rates of classic solvers [ ] (i.e. $\|m-x\|\leq Ch^q$ for $q\geq 1$)
- produce posterior variance estimates that are calibrated worst-case error estimates [ ] (i.e. $\|m-x\|^2\leq Ck$). In Short, they produce meaningful uncertainty
- are in fact a generalization of certain famous classic ODE solvers (namely they reduce to explicit single-step Runge Kutta methods and multi-step Nordsieck methods in the limit of uninformative prior and steady-state operation, respectively. In practical operation, they offer a third, novel type of solver) [ ]
- they can be generalized to produce non-Gaussian, nonparametric output while retaining many of the above properties [ ].
Together, these results provide a rich and reliable new theory for probabilistic simulation that current ongoing research projects are seeking to leverage to speed up structured simulation problems inside of machine learning algorithms.
