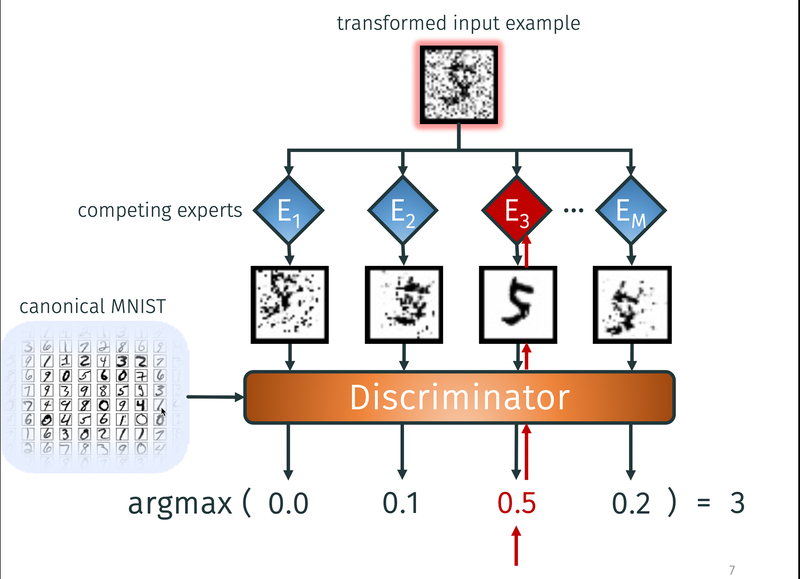
Through a competition of experts, inverse causal mechanisms are learned as independent modules in an image task. This results in generalisable and broadly applicable network modules, which can subsequently be combined and applied to new domains.
In the terminology of a book we recently published [ ], the term causal inference comprises both causal reasoning and causal discovery, two somewhat inverse scenarios: While the former employs causal modelds for inferring about the expected observations (often, about their statistical properties), the latter is concerned with inferring causal models from empirical data. Both parts crucially depend on assumptions on the statistical properties entailed by hypothetical causal structures. During the past decade various assumptions have been proposed and assayed that go beyond traditional assumptions like the causal Markov condition and causal faithfulness. This has implications for both scenarios: it improves identifiability of causal structure, and it also entails additional statistical predictions if the causal structure is known.
Traditional causal discovery assumes that the units are connected by a causal directed acyclic graph a priori (mostly as random variables). In contrast, real-world observations are not necessarily a priori structured into those units (e.g. objects in images). The task of identifying reasonable units that admit causal models is challenging for both human and machine intelligence, but it aligns with the general goal of modern machine learning to learn meaningful representations for data, where `meaningful' can for instance mean interpretable, robust, or transferable. The general idea that causal structure is a concept that often remains invariant across changing background conditions (first discussed by Herb Simon, and discussed in detail in our book) can be utilized for both causal reasoning and causal discovery. Identifying causal units will therefore be a third subsection below.
Causal reasoning:
Subject to sufficiently specific model assumptions (here: additive independent noise), causal knowledge admits novel techniques of noise removal such as our method of half-sibling regression published in PNAS [ ], applied to astronomic data from NASA's Kepler space telescope [ ].
Apart from entailing statistical properties for a fixed distribution, causal models also suggest how distributions change across data sets. To this end, one may assume, for instance, that structural equations remain constant across data sets and only the noise distributions change [ ], that some of the causal conditionals in a causal Bayesian network change, while others remain constant [ ], or that they change independently [ ], which results in new approaches to domain adaptation [ ].
Causal discovery:
The toy problem of telling cause from effect in bivariate distributions, which we have earlier shown to be insightful also for more general causal inference problems, has been further explored [ ]. The performance of a broad variety of new approaches has been extensively studied in a long JMLR paper [ ], suggesting that classification of cause and effect is indeed possible above chance level. New results for the multi-variable setting deal with, for instance, the problem of learning structural equation models in the presence of selection bias [ ] and the idea of employing generalized score functions [ ]. [ ] introduces a kernel-based statistical test for joint independence of random variables which is a key component of multi-variate additive noise based causal inference.
Apart from progress on those 'classical' causal inference problems the domain of causal inference has been extended in several directions. Causal discovery for rare events has been further developed in terms of interacting Hawkes processes [ ]. To study causal signals in images, the CVPR paper [ ] infers whether the presence of an object on an image is the cause or the effect of the presence of another one, using additive noise based cause-effect inference.
In a study connecting principles of causal inference and foundations of physics [ ], we relate asymmetries between cause and effect to asymmetries between past and future, deriving the thermodynamic arrow of time from the basic assumption of (algorithmic) independence of causal mechanisms. Within machine learning and time series modeling, new causal inference methods have revealed previously unknown aspects of the arrow of time [ ].
Identifying causal units and causal learning:
Defining objects that are related by causal models typically amounts to appropriate coarse-graining of more detailed models of the world (e.g., physical models). Subject to appropriate conditions, causal models like structural equation models can arise from coarse-graining of `microscopic' models including microscopic structural equation models [ ], ordinary differential equations [ ], temporally aggregated time series [ ], or temporal abstractions of recurrent dynamical models [ ]. Although every causal models in economics, medicine, or psychology uses variables that are abstractions of more elementary concepts, it is challenging to state general conditions under which coarse-grained variables admit causal models with well-defined interventions. Our work [ ] provides some sufficient conditions.
Theoretical work in [ ] shows that the independence of causal mechanisms can be formalized via group symmetry. The plausibility of a scene inferred from an image, for instance, can be formally assessed by testing whether some 'contrast function' attains values that are typical among those reached by symmetry transformations. This way, statistical independence (with permutations as corresponding symmetry group) is just a special case of a more general notion of independence.
In the context of a classical image recognition task, our recent ICML paper [ ] shows that learning causal models that contain invariant mechanisms helps in transferring information across substantially different data sets (see figure). We plan to further pursue this direction, with the goal of moving from statistical representation learning towards causal world representations that should be more robust and support notions of intervention and planning.
Causal Representation Learning
Deep neural networks have achieved impressive success on prediction tasks in a supervised learning setting, provided sufficient labelled data is available. However, current AI systems lack a versatile understanding of the world around us, as shown in a limited ability to transfer and generalize between tasks.
| The course focuses on challenges and opportunities between deep learning and causal inference, and highlights work that attempts to develop statistical representation learning towards interventional/causal world models. The course will include guest lectures from renowned scientist both from academia as well as top industrial research labs. |
The course covers amongst others the following topics:
- Causal Inference and Causal Structure Learning
- Deep Representation Learning
- Disentangled Representations
- Independent Mechanisms
- World Models and Interactive Learning
Grading
The seminar is graded as pass/fail. In order to pass the course, participants need to write a summary of at least one lecture (n lectures if the team consists of n team members) and write reviews for at least two submissions (2*n reviews if the team consists of n team members). Course summaries and reviews will have to be submitted through openreview (link to be provided). For the assignment to a particular lecture a survey will be sent around. The course summary has to follow the NeurIPS format, however with 4 pages of text (references and appendix are limited to an additional 10 pages). Please find the template for the seminar below.
Seminar template: Download
The submission deadline: January 15, 2021.
Time and Place
|
Lectures |
Tue, 16:00-18:00 |
Online |
The zoom link for the online lectures will be send by email to registered students at ETH. If you have not done so please register for the course.
Questions
If you have any questions, please use the Piazza group: piazza.com/ethz.ch/
Please submit your lecture notes here: https://openreview.net/group?
Lecture notes: Download (Disclaimer: These summaries were written by students have not been reviewed / proofread by the lecturers).
Syllabus
| Day | Lecture Topics | Lecture Slides | Recommended Reading | Background Material |
| Sep 15 | Introduction | Lecture 1 | Elements of Causal Inference |
Pearl, Judea, and Dana Mackenzie. The book of why: the new science of cause and effect. Basic Books, 2018. |
| Sep 22 | Lecture 2 | Elements of Causal Inference | ||
| Sep 29 |
|
Lecture 3 | Elements of Causal Inference | |
| Oct 6 | Lecture 4 | Guest: Sebastian Weichwald | ||
| Oct 13 | Lecture 5 | Guest: Francesco Locatello | ||
| Oct 20 | Lecture 6 | Opening AI Center - no lecture | ||
| Oct 27 | Lecture 7 | Guest: Ilya Tolstikhin | ||
| Nov 3 | Lecture 8 | Guest: Irina Higgins | ||
| Nov 10 | Lecture 10 | Guest: Patrick Schwab | ||
| Nov 17 | Lecture 11 | Guest: Ferenc Huszár | ||
| Nov 24 | Lecture 12 | Guest: Patrick Schwab | ||
| Dec 1 | Lecture 13 | Guest: Anirudh Goyal | ||
| Dec 20 | Lecture 14 | Guest: Silvia Chiappa |
Primary References
B. Schölkopf. "Causality for machine learning." arXiv preprint arXiv:1911.10500 (2019).
J. Peters, D. Janzing, and B. Schölkopf. Elements of causal inference. The MIT Press, 2017.
Additional references
Pearl, Judea. Causality. Cambridge university press, 2009.
Hernán, Miguel A., and James M. Robins. "Causal inference: what if." Boca Raton: Chapman & Hill/CRC 2020 (2020).
2018
Neitz, A., Parascandolo, G., Bauer, S., Schölkopf, B.
Adaptive Skip Intervals: Temporal Abstraction for Recurrent Dynamical Models
Advances in Neural Information Processing Systems 31 (NeurIPS 2018), pages: 9838-9848, (Editors: S. Bengio and H. Wallach and H. Larochelle and K. Grauman and N. Cesa-Bianchi and R. Garnett), Curran Associates, Inc., 32nd Annual Conference on Neural Information Processing Systems, December 2018 (conference)
Rojas-Carulla, M., Schölkopf, B., Turner, R., Peters, J.
Invariant Models for Causal Transfer Learning
Journal of Machine Learning Research, 19(36):1-34, 2018 (article)
Parascandolo, G., Kilbertus, N., Rojas-Carulla, M., Schölkopf, B.
Learning Independent Causal Mechanisms
Proceedings of the 35th International Conference on Machine Learning (ICML), 80, pages: 4033-4041, Proceedings of Machine Learning Research, (Editors: Dy, Jennifer and Krause, Andreas), PMLR, July 2018 (conference)
Huang, B., Zhang, K., Lin, Y., Schölkopf, B., Glymour, C.
Generalized Score Functions for Causal Discovery
Proceedings of the 24th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), pages: 1551-1560, (Editors: Yike Guo and Faisal Farooq), ACM, August 2018 (conference)
Besserve, M., Shajarisales, N., Schölkopf, B., Janzing, D.
Group invariance principles for causal generative models
Proceedings of the 21st International Conference on Artificial Intelligence and Statistics (AISTATS), 84, pages: 557-565, Proceedings of Machine Learning Research, (Editors: Amos Storkey and Fernando Perez-Cruz), PMLR, April 2018 (conference)
Blöbaum, P., Janzing, D., Washio, T., Shimizu, S., Schölkopf, B.
Cause-Effect Inference by Comparing Regression Errors
Proceedings of the 21st International Conference on Artificial Intelligence and Statistics (AISTATS) , 84, pages: 900-909, Proceedings of Machine Learning Research, (Editors: Amos Storkey and Fernando Perez-Cruz), PMLR, April 2018 (conference)
Pfister, N., Bühlmann, P., Schölkopf, B., Peters, J.
Kernel-based tests for joint independence
Journal of the Royal Statistical Society: Series B (Statistical Methodology), 80(1):5-31, 2018 (article)
Rubenstein, P. K., Bongers, S., Schölkopf, B., Mooij, J. M.
From Deterministic ODEs to Dynamic Structural Causal Models
Proceedings of the 34th Conference on Uncertainty in Artificial Intelligence (UAI), pages: 114-123, (Editors: Globerson, Amir and Silva, Ricardo), August 2018 (conference)
2017
Huang, B., Zhang, K., Zhang, J., Sanchez-Romero, R., Glymour, C., Schölkopf, B.
Behind Distribution Shift: Mining Driving Forces of Changes and Causal Arrows
IEEE 17th International Conference on Data Mining (ICDM), pages: 913-918, (Editors: Vijay Raghavan,Srinivas Aluru, George Karypis, Lucio Miele and Xindong Wu), November 2017 (conference)
Rubenstein*, P. K., Weichwald*, S., Bongers, S., Mooij, J. M., Janzing, D., Grosse-Wentrup, M., Schölkopf, B.
Causal Consistency of Structural Equation Models
Proceedings of the 33rd Conference on Uncertainty in Artificial Intelligence (UAI), pages: ID 11, (Editors: Gal Elidan, Kristian Kersting, and Alexander T. Ihler), August 2017, *equal contribution (conference)
Gong, M., Zhang, K., Schölkopf, B., Glymour, C., Tao, D.
Causal Discovery from Temporally Aggregated Time Series
Proceedings of the 33rd Conference on Uncertainty in Artificial Intelligence (UAI), pages: ID 269, (Editors: Gal Elidan, Kristian Kersting, and Alexander T. Ihler), August 2017 (conference)
2016
Zhang, K., Hyvärinen, A.
Nonlinear functional causal models for distinguishing cause from effect
In Statistics and Causality: Methods for Applied Empirical Research, pages: 185-201, 8, 1st, (Editors: Wolfgang Wiedermann and Alexander von Eye), John Wiley & Sons, Inc., 2016 (inbook)
Janzing, D., Chaves, R., Schölkopf, B.
Algorithmic independence of initial condition and dynamical law in thermodynamics and causal inference
New Journal of Physics, 18(9):article no. 093052, 2016 (article)
Wang, D., Hogg, D. W., Foreman-Mackey, D., Schölkopf, B.
A Causal, Data-driven Approach to Modeling the Kepler Data
Publications of the Astronomical Society of the Pacific, 128(967):094503, 2016, Astrophysics Source Code Library ascl: 2107.024 (article)
Bauer, S., Schölkopf, B., Peters, J.
The Arrow of Time in Multivariate Time Serie
Proceedings of the 33rd International Conference on Machine Learning (ICML), 48, pages: 2043-2051, JMLR Workshop and Conference Proceedings, (Editors: Balcan, M. F. and Weinberger, K. Q.), JMLR, June 2016 (conference)
Zhang, K., Zhang, J., Huang, B., Schölkopf, B., Glymour, C.
On the Identifiability and Estimation of Functional Causal Models in the Presence of Outcome-Dependent Selection
Proceedings of the 32nd Conference on Uncertainty in Artificial Intelligence (UAI), pages: 825-834, (Editors: Ihler, Alexander T. and Janzing, Dominik), June 2016 (conference)
Etesami, S., Kiyavash, N., Zhang, K., Singhal, K.
Learning Network of Multivariate Hawkes Processes: A Time Series Approach
Proceedings of the 32nd Conference on Uncertainty in Artificial Intelligence (UAI), pages: 162-171, (Editors: Ihler, Alexander T. and Janzing, Dominik), June 2016 (conference)
Gong, M., Zhang, K., Liu, T., Tao, D., Glymour, C., Schölkopf, B.
Domain Adaptation with Conditional Transferable Components
Proceedings of the 33nd International Conference on Machine Learning (ICML), 48, pages: 2839-2848, JMLR Workshop and Conference Proceedings, (Editors: Balcan, M.-F. and Weinberger, K. Q.), June 2016 (conference)
Peters, J., Bühlmann, P., Meinshausen, N.
Causal inference using invariant prediction: identification and confidence intervals
Journal of the Royal Statistical Society, Series B (Statistical Methodology), 78(5):947-1012, 2016, (with discussion) (article)
Mooij, J., Peters, J., Janzing, D., Zscheischler, J., Schölkopf, B.
Distinguishing cause from effect using observational data: methods and benchmarks
Journal of Machine Learning Research, 17(32):1-102, 2016 (article)
Schölkopf, B., Hogg, D., Wang, D., Foreman-Mackey, D., Janzing, D., Simon-Gabriel, C. J., Peters, J.
Modeling Confounding by Half-Sibling Regression
Proceedings of the National Academy of Science, 113(27):7391-7398, 2016 (article)




